Invers Dan Determinan Matriks ~ Zona E-Pelajar

Mencoba memenuhi permintaan dari sobat Bryan untuk posting tentang invers dan determinan matriks, maka pada postingan kali ini akan mencoba membahas sedikit materi yang berkaitan dengan invers dan determinan matriks.

Matriks merupakan susunan bilangan-bilangan berbentuk persegi atau persegi panjang yang diatur menurut baris dan kolom tertentu. Matriks dinotasikan dengan huruf kapital. Jika m adalah banyaknya baris dari matriks $A$ , dan n adalah banyaknya kolom dari matriks $A$ , maka matriks $A$ mempunyai ordo $m \times n$ , atau ditulis $A_{m\times n}$ .

$A_{m \times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \cdots &\vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}$

1. Invers Matriks

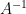Jika A dan B adalah matriks persegi, dan berlaku $A \cdot B = B \cdot A = I$ maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis $A^{-1}$ . Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.

Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini.
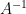Jika $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ dengan $ad - bc \neq 0$ , maka invers dari matriks A (ditulis $A^{-1}$ ) adalah sebagai berikut:

$A^{-1} = \frac {1}{ad - bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$

Jika $ad - bc = 0$ maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.

Sifat-sifat matriks persegi yang mempunyai invers:

- $(A \cdot B)^{-1} = B^{-1} \cdot A^{-1}$
- $(B \cdot A)^{-1} = A^{-1} \cdot B^{-1}$
- $(A^{-1})^t =(A^{t})^{-1}$

Contoh: Tentukan invers dari matriks berikut!

$\begin {array} {lcl} A & = & \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \\ A^{-1} & = & \frac {1}{2 \times 3 - 1 \times 5} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ & = & \frac {1}{6-5} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ & = & \frac {1}{1} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ A^{-1} & = & \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix}\end{array}$

2. Determinan Matriks

Syarat suatu matriks dapat dicari determinannya adalah matriks tersebut harus merupakan matriks persegi. Jika $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ , maka rumus untuk mencari determinan matriks berordo 2×2:

$det A = \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc$

Sedangkan untuk mencari determinan matriks berordo 3×3 menggunakan aturan Sarrus.

$A_{3 \times 3} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{2n}\\ a_{31} & a_{32} & a_{33} \end{bmatrix}$

$\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{2n}\\ a_{31} & a_{32} & a_{33} \end{vmatrix} \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{matrix}$

$\begin{array} {lcl} \begin{vmatrix} A \end{vmatrix} = && a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\ & - & a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \end{array}$

Contoh: Tentukan determinan dari matriks berikut!

$A = \begin{bmatrix} 3 & 1 \\ 5 & 2 \end{bmatrix}$

$\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 \\ 5 & 2 \end{vmatrix} = 3 \times 2 - 1 \times 5 = 6 - 5 = 1$

$B = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 3 & 4\\ 1 & 4 & 3 \end{bmatrix}$

$\begin{vmatrix} B \end{vmatrix} = \begin{vmatrix}1 & 2 & 3 \\ 1 & 3 & 4\\ 1 & 4 & 3 \end{vmatrix} \begin{matrix} 1 & 2\\ 1 & 3 \\ 1 & 4 \end{matrix}$

$\begin{array} {lcl} \begin{vmatrix} B \end{vmatrix} & = & 1.3.3 + 2.4.1 + 3.1.4 - 1.3.3 - 4.4.1 - 3.1.2 \\ & = & 9 + 8 + 12 - 9 - 16 - 6 \\ & = & -2 \end{array}$

Zona E-Pelajar

Popular Posts

Tukar Link Yuk

E-Vid

E-News

Traffic Info

Sabtu, 31 Desember 2011